어린이과학동아&수학동아 연재기사

알람브라 궁전이 규칙적인 무늬로 유명해진 데에는 또 다른 이유가 있어.

바로 ‘테셀레 이션’, 우리말로는 ‘쪽매맞춤’ 덕분이야.

같은 모양의 조각들로 공간을 겹치지 않게 빈 틈없이 채우는 것을 테셀레이션이라고 하지.

우리가 주위에서 쉽게 볼 수 있는 벌집이나 보도블록에서도 찾아볼 수 있어.

테셀레이션을 만들려면 모양 사이에 빈틈이 없어야 한다고 했지?

그러려면 모양의 꼭짓점이 만나는 각을 합쳤을 때 360°가 돼야 해.

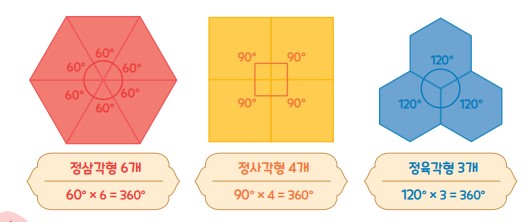
정삼각형, 정사각형, 정육각형을 이어 붙이면 각각 테셀레이션을 만들 수 있어.

한 각의 크기가 60°인 정삼각형 6개가 만 나면 360°, 한 각의 크기가 90°인 정사각형 4개가 만나면 360°, 한 각의 크기가 120°인 정육각형 3개가 만나면 360°야.

다른 정다각형으로도 테셀레이션을 만들 수 있을까?

아쉽게도, 360°를 만드는 다른 정다 각형은 없어.

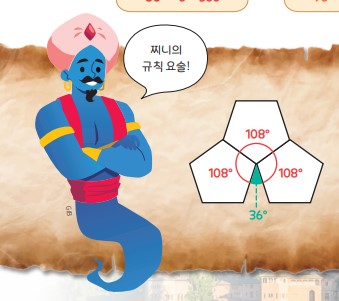
예를 들어 정오각형으로 테셀레이션을 만든다고 생각해 봐.

정오각형 한 각의 크기는 108°야.

각이 맞닿는 부분의 합은 108+108+108 = 324°로, 360°보다 36° 가 부족해서 빈틈이 생겨.

짠! 오른쪽 알람브라 궁전의 벽도 빈틈없이 딱 들어맞는 테셀레이션이야.

잘 보면 색이 칠해진 무늬와 사이사이에 있는 흰색 무늬가 서로 같은 모양이라는 걸 알 수 있어.

그런데 어떻게 테셀레이션이 될 수 있을까?

바로 모양을 비틀어도 꼭짓점이 만나는 각의 합은 360°라는 점을 활용했기 때문이야.

이 벽 무늬는 삼각형을 비틀어서 만들었어.

삼각형은 조금 비틀어도 빈틈없이 모든 각이 맞닿아 있어.

이렇게 전부 같은 회오리 삼각형 모양으로 변신시키고, 무늬 가운데 에 육각형과 별 모양을 장식해 이어 붙이면 테셀레이션 완성!

훨씬 화려한 무늬로 탈바 꿈했어!

알람브라 궁전 속 개성 넘치는 무늬들의 규칙을 알았으니, 이제 너희가 직접 무늬의 규칙을 찾아볼래?

어떤 모양이 반복되는지, 어떤 방법으로 이동하는지를 알면 규칙을 바로 찾을 수 있다는 사실, 잊지 마!