어린이과학동아&수학동아 연재기사

안녕? 나는 <어수동> 친구들에게만 나타나는 수의 정령 ‘수르’야.

먼 옛날부터 지금까지 숫자에 관한 것이라면 모두 지켜봤지.

물론, 호루스의 눈 조각도 자세히 살펴봤어.

호루스의 눈 조각 6개에는 각각을 상징하는 ‘분수’가 있더라.

어떤 분수인지 궁금하면 내 이야기를 따라와!

 

분 수가 언제 처음 등장했는지는 정확히 알려지지 않았지만,

아마도 지금으로부터 약 370 0년 전부터 분수를 사용했을 것으로 추측돼.

가장 오래된 수학책으로 알려진 3700년 전의 책 ‘아메스 파피루스’에 고대 이집트인들이 실생활 에서 분수를 어떻게 사 용했는지 적혀 있거든.

고대 이집트에서는 일한 대가로 돈 대신 빵을 받았어.

그런데, 일한 사람은 3명이고 주어진 빵은 1개일 때 한 사람에게 각각 돌아가는 빵의 양은 얼마인 

지를 숫자로 나타낼 수가 없었어.

그래서 새로운 수인 분수를 만들었지.

1, 2, 3,… 같은 자연수로 나타낼 수 없는 양을 표현하기 위해서야.

당시에는 지금 우리가 사용하는 숫자가 없었고, 수를 그림으로 나타냈지. 

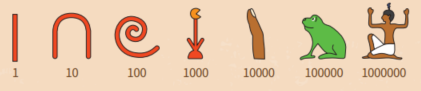
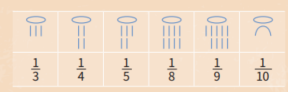
분수를 쓸 때는 수를 나타내는 그림 위에 입 모양을 그렸어.

예를 들어 숫자 3을 나타내는 작대기 3개 위에 입 모양이 있으면  1/3인 거야.

입 모양 그림이 지금의 분수에 있는 선분과 같은 역할을 한 거지.

그런데, 왜 ‘분자’를 나타내는 그림은 없었을까?

 

고대 이집트인들은 ‘단위분수’를 사용했어. 

단위분수는 1/2 , 1/3처럼 분자가 1인 분수를 말해. 

그래서 이집트인들이 분수를 그림으로 나타낼 때 분자는 따로 그릴 필요가 없었던 거야. 

이집트인들은 2/3 , 5/6 같은 모든 분수를 단위분수의 덧셈으로 나타냈어. 

이집트인들의 분수 계산법을 한번 볼까?

 

 

빵 2개를 3명이 나눠 가질 때, 1명이 먹을 수 있는 빵의 양은 2/3이다. 

하지만 이집트 사람들은 이를 2/3라고 나타내지 않고, 1/2 + 1/6 으로 나타냈다.

 

 

 

자, 이제 다시 ‘호루스의 눈’ 이야기를 들려줄게. 

이집트인들은 호루스의 눈이 ‘완전함’의 상징이라고 생각해서, 눈 전체를 숫자 ‘1’로 생각했어. 

이집트인들은 6개의 조각으로 나뉜 호루스의 눈에 단위분수를 하나씩 배치하고, 이들의 합이 1이 되게 했어.

 

각 단위분수를 합치면 정말 1이 되는지 볼까? 

분수를 더하려면 분모가 서로 같아야 하니까, 분모가 모두 64가 되도록 분모와 분자에 각각 같은 수를 곱해.

분모가 모두 같아진 다음에는, 분자의 수끼리 더하면 끝이야.

 

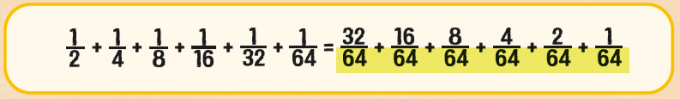
(32+16+8+4+2+1)/64 = 63/64 ! 

그런데 1/64 이 모자라지 않냐고? 

이집트인들은 부족한 1/64 을 지혜의 신인 토트가 채워준다고 생각했거든. 

토트가 마지막 1/64 을 더해주면, 호루스의 눈은 완전한 1이 되는 거야!

 

어때, 분수 이야기 재미있지? 

고대 중국의 수학책 ‘구장산술’에도 분수가 등 장하는 것을 보면,

분수는 아주 오래전부터 여러 나라에서 사용됐을 거야. 

다음에도 만난다면, 또 다른 이야기를 들려줄게. 

안녕~!